Last edit: 26/06/2023

IEC 62061 uses the following main parameters.
- λ: Failure rate
- MTTF: Mean Time to Failure
- SFF: Safe Failure Fraction
- HFT: Hardware Fault Tolerance
Failure Rate
It is the basis of the IEC 61508 and therefore of IEC 62061. We can borrow its definition from IEC 61508-4:
3.6.16 failure rate. Reliability parameter (λ(t)) of an entity (single components or systems) such that λ(t)•dt is the probability of failure of this entity within [t, t+dt] provided that it has not failed during [0, t]
Mathematically, λ(t) is the conditional probability of failure per unit of time over [t, t+dt].
It is in strong relationship with the Reliability Function:
In order to use IEC 62061, each component used in the SCS should have a Failure rate value. In Low demand that is normally the case. In high demand, a lack of direct data has contributed to the limited use of the standard so far.
Failures can be divided in 4 parts:
λS: rate of safe failures
λD: rate of dangerous failures (λ x proportion of dangerous failures)
λDD: rate of dangerous failure which is detected by the diagnostic functions
λDU: rate of dangerous failure which is NON detected by the diagnostic functions
Ʃ λS + Ʃ λD is the overall failure rate
In High Demand, only the Dangerous failures are considered. The Detectable part is calculated as λDD=DC λD while the undetectable part as λDU=(1-DC) λD
MTTFd
The Mean Time to Failure (MTTFD) is a parameter used for non-reparable components.
It is the expected time when 63,2% of the components under test have failed dangerously. It is a statistical parameter: if the MTTFD for a solenoid valve is 30 years, it does not mean that it is guaranteed for 30 years. It simply means that, if we consider for example 100 valves, after 30 years 63 have failed; however if you bought one of those 100 valves, it may fail after 1 month.
The MTTFD, as weel as the λD, are valid only for the Useful Lifetime of the component, that is normally 20 years. Beyond that time, the parameters lose significance, since the failure rates cannot be considered constant anymore. That means if an hydraulic Valve has a MTTFD of 150 years, it can be used only for 20 years for safety related operations. After that time it has to be replaced.
Safe Failure Function – SFF
The Safe Failure Fraction (SFF) was introduced in IEC 61508 as a measure used to determine the minimum Hardware Fault Tolerance (HFT) of a safety subsystem. Hereafter its definitions:
[IEC 62061] 3.2 Terms and definitions
3.2.56 Safe Failure Fraction (SFF). fraction of the overall failure rate of a subsystem that does not result in a dangerous failure.
At a first sight, the definition of IEC 62061 does not seem right; but please consider that dangerous detectable failures, since they are detectable, will not generate any dangerous situation: that is the reasoning behind the definition. SFF is used in both high and low demand mode with the same meaning.
Considering that the random hardware failures of IEC 61508 are based upon the various types of failure rates of a component, SFF is an indication of how “transparent” the failures are. In other terms the lower is the percentage of Dangerous Undetected failure, the higher is the SFF.
Here the way it is calculated:
The SFF is the proportion of “safe” failures among all failures. A “safe” failure is either a failure that is safe by design, or a dangerous failure that is immediately detected and corrected. The IEC standards define a safe failure as a failure that does not have the potential to put the SIS in a hazardous or fail-to-function state. A dangerous failure is a failure that can prevent the SIS from performing a specific SIF, but when detected soon after its occurrence, for example by online diagnostics, the failure is considered to be “safe” since the Diagnostics can bring the system to a safe state.
Many electronic safety devices have built-in diagnostics such that most dangerous failures become Dangerous Detectable failures and they will therefore have a high SFF, often greater than 90%. Mechanical safety devices, for which internal diagnostics is not feasible, will have, in general, a low SFF.
Hardware Fault Tolerance – HFT
The concept Hardware Fault Tolerance (HFT) is used in IEC 61508 to indicate the ability of a hardware subsystem to continue performing a required function, in the presence of faults or errors. The HFT is given as a digit, where HFT = 0 means that if there is one fault, the function (e.g., to measure pressure) is lost. HFT = 1 means that if a channel fails, there is one other channel that is able to perform the same function, or that the subsystem can tolerate one failure and still be able to function. A subsystem of three channels that are voted 2oo3 is functioning as long as two of its three channels are functioning. This means that the subsystem can tolerate that one channel fails and still function as normal. The Hardware Fault Tolerance of the 2oo3 voted group is, therefore, HFT = 1.
Let’s now look at its definition:
[IEC 62061] 3.2 Terms and definitions
3.2.36 Hardware Fault Tolerance (HFT). Property of a subsystem to potentially lose the safety function upon at least N+1 faults.
The architecture of the control system and the "safe failure fraction" (SFF) play an important role in EN 62061. The Hardware Safety Integrity level that can be claimed for a subsystem is limited not only by the PFHD but also by the Hardware Fault Tolerance and Safe Failure Fraction.
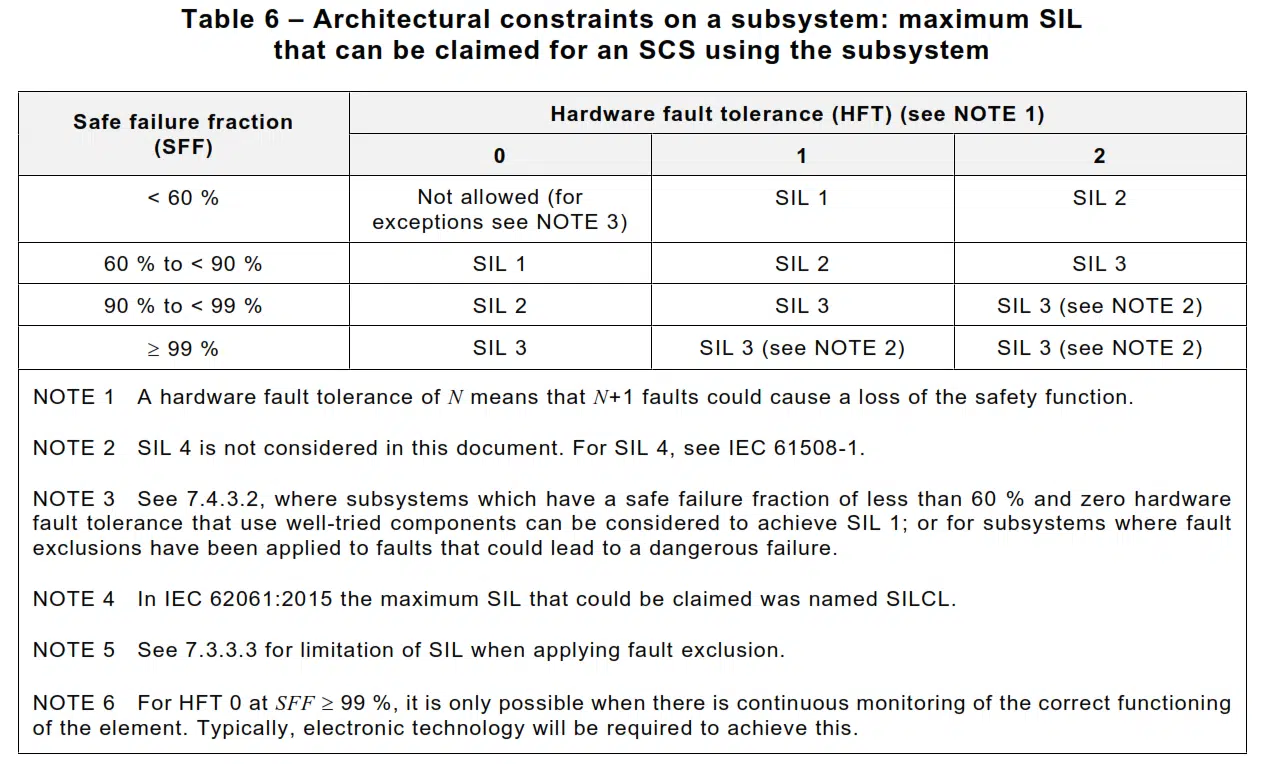
The combination of these two elements is defined in the new 2021 edition of the standard as the Architectural Constraints and its output is the maximum SIL that the safety subsystem can reach (once called Sil Claim or SIL CL).
Table 6 of the 2021 edition details the maximum SIL that a component can reach, based upon its Safe Failure Fraction and HFT. As it can be seen, if a 1oo1 Subsystem (Basic Subsystem Architecture A or HFT=0) has a very low percentage of dangerous undetected failure (meaning a high SFF), its subsystem can reach SIL 2 or even SIL3. In the new edition it is made clear that, in case of Electromechanical components, that is highly unlikely.