Last edit: 07/08/2023
The failure rate is the basis of the Functional Safety theory.
[IEC 61508-4] 3.6 Fault, failure and error
3.6.16 Failure rate. Reliability parameter λ(t) of an entity (single components or systems) such that λ(t)dt is the probability of failure of this entity within [t, t+dt] provided that it has not failed during [0, t].
Mathematically, λ(t) is the conditional probability of failure per unit of time over [t, t+dt]. It is possible to demonstrate that the instantaneous failure rate is:
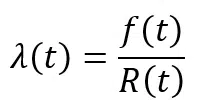
Using the equation , it is possible to obtain:
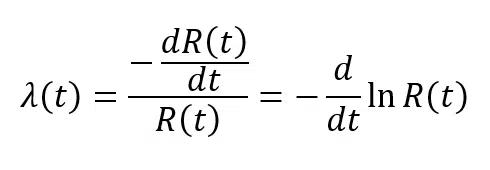
Integrating the upper equation in time:
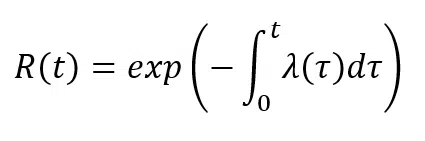
Failure rates and their uncertainties can be estimated from field feedback, using conventional statistics.
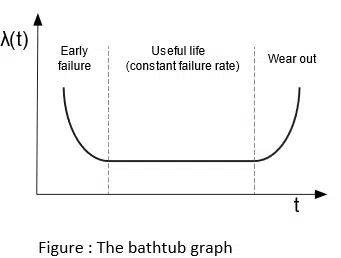
The most diffuse and widely known model for the failure rate is the “bathtub” curve. In the initial phase of the component lifetime, λ(t) decreases rapidly with time; this fact derives from the existence of a “weak” fraction of the population whose defects cause a failure within a short period of time from the moment they are produced.
In the period called useful life, λ(t) is approximately constant, in case for example, of electronic components. For electromechanical components, λ(t) is a function of time and, in this interval, it constantly increases.
The last period is characterised by a wear out, with a rapidly increasing failure rate λ(t) caused by the wearing out, aging and fatigue.
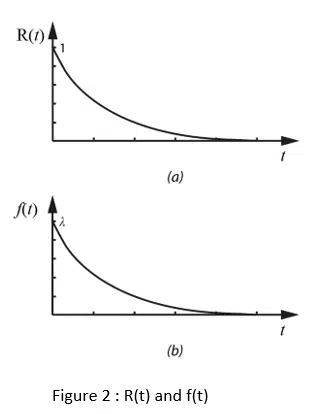
During the useful life of a component with a constant failure rate, considering as an initial condition that Reliability at time 0 is at a maximum and it is equal to 1, we have:
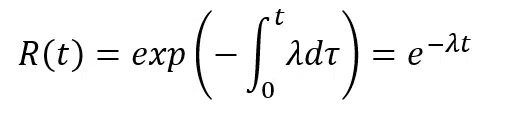
The Reliability function R(t) is shown in Figure 2a and the Probability Density Functions f(t) in Figure 2b , in the case λ = constant.
Table 1 shows a summary of the four functions described so far.

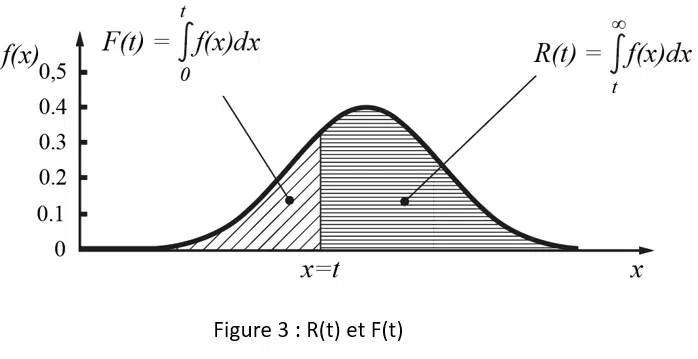
Figure 3 shows the relationship between F(t) and R(t)