Last edit: 07/08/2023
The PFD(t) is the unreliability function F(t) used in low demand mode. Hereafter its definition, supposing a constant failure rate λ:
[IEC 61508-4] 3.6 Fault, failure and error
3.6.17 Probability of dangerous failure on demand (PFD). Safety unavailability (see IEC 60050-191) of an E/E/PE safety-related system to perform the specified safety function when a demand occurs from the EUC or EUC control system
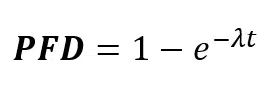
Therefore, the instantaneous unreliability PFD (t) describes the probability that a safety system is not in a state to perform its required function, under given conditions, at a given instant of time, assuming that the required external resources are provided. Again, it is what we called so far F(t).
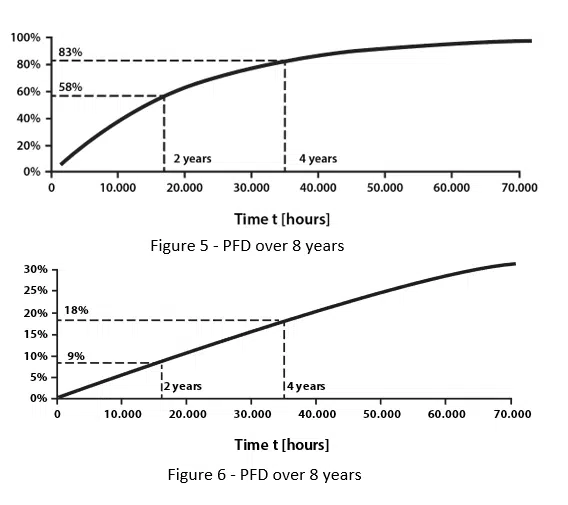
Considering, for example, a valve with a λ = 50.000 FIT, its PFD(t) is shown in figure 5. As you can see, the Unreliability increases with time; after 2 years (17520 hours), PFD≈58%. After 4 years (35040 hours), PFD≈83%.
Considering a λ = 5.000 FIT, a more realistic value, its PFD(t) is shown in figure 6. First of all, the PFD has improved: after 2 years, PFD ≈ 9% and after 4 years, PFD ≈ 18%. Moreover, the function can be approximated to a linear one, in case λ·t << 1.
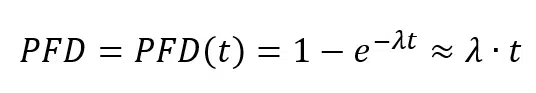
As it can be seen from both graphs, the System unreliability increases with time. Going back to the example of the airbag, that means its probability of failure will be very low when the car is new and it will increase month by month. That is valid for all the elements of a Safety Instrumented System (SIS), that is made by one or more sensors, a logic unit and one or more actuators.