Last edit: 04/08/2025
Summary

Within this article, the main international standards involved in Functional Safety and how they apply the Reliability Engineering Theory are investigated.
In particular, the feasibility of the Reliability Block Diagrams (RBDs) method is evaluated by analyzing the models used in the normative and comparing them with the results obtainable through the Markov chain model.
The RBD strategy is then used to study a structure not investigated by the standards: the double channel with diagnostic external to the functional channel.
The results, despite the approximations and simplifications introduced by the model under consideration, allow a preliminary solution to be provided for this structure, consistent with the range of expected results, that confirms the flexibility of the tool presented, which may be a future method to delineate the perimeter of more complex models.
Introduction
Functional Safety represents a portion of the risk reduction procedure associated with a machine or process protected by the implementation of a Safety Control System (SCS).
The development of these safety-critical systems requires much effort since the final objective is the safe condition: represented by the elimination of all residual energies, which could cause injuries to people, harms to things or repercussions on the environment.
A deep understanding of the standards involved, how these apply the Reliability Engineering theory and the models that develop, is in the scope of this article.
Reliability Engineering
The discipline that studies the ability of a system or component to perform a required function, under specified conditions and for a given time interval, without failing, is the Reliability.
In this theory, Failures are classified as either random or systematic. The firsts can be characterized by statistical parameters while the seconds by means of a qualitative management approach in all the lifecycle of the component.
One of the possible analytical methods to assess the Reliability of a system is the Reliability Block Diagram (RBD): a static illustration by means of functional blocks, which can be treated as Boolean variables equations and their Reliability calculated as the overall probability of success/failure.
Key Parameters in Functional Safety Theories
The focus is to guarantee adequate performance, during the mission time, of the components involved in the safety functions; to achieve the specifications defined during the risk assessment.
Two functions could be used to assess the Unreliability of an item or system, defined as the probability that the item or system stops its required function at a certain time and linked to the Reliability by equation (1).

- In low demand, the parameter used to indicate the Unreliability of a safety function is the Average Probability of Dangerous Failure on Demand 〖PFD〗_avg, equation (2)

- In High Demand mode of operation, the Unreliability is specified by the Average Frequency of a Dangerous Failure per Hour (or), equation (3).

The distinction between low and high demand, is quantified by the normative in the value of one request per year.
Standards about Functional Safety
IEC 61508 is the principal of all Functional safety product standards.
It allows the Electrical/Electronic/Programmable Electronic Systems (E/E/PS) to be applied as safety critical items, specifying four levels of safety performance (from 1 to 4) called Safety Integrity Levels (SIL).
Two international standards deal with the concept of functional safety applied to machinery: the first is IEC 62061, derived from IEC 61508 and the second is ISO 13849.
Both concentrates on high demand and continuous mode of operations. The quantification of the reduction of risk operated is measured for IEC in SIL and for ISO in Performance Levels (PL), a relation between the two units is reported in table 1.

Table 1: Relationship between performance levels (PL) and safety integrity levels (SIL).
The normative related to process industry is IEC 61511, which does not contain any formula but defines what must be achieved to meet the requirements of IEC 61508 in a process sector application (typically in low demand mode of operation).
The highest level that can be claimed by a safety related control system (SCS) is limited by a combination of redundancy, detection and component reliability.
To facilitate the design or the assessment of the achieved SIL or PL, the standards employ a methodology based on the categorization of architectures, with specific design criteria and behaviour under faults conditions (redundancy). These categories represent the ways in which achieve a specific SIL or PL of a subsystem, in other terms they describe the required behaviour of the subsystem with respect to its resistance to faults.
Calculation Models Involving RBD
Except ISO 13849-1, which applies Markov chains models, the standards analyzed deal with the quantification of safety parameters using Reliability Block Diagrams (RBDs).
IEC 61508-6 provides approximation formulas for the and (low and high demand mode of operations) of simple configurations with no more than three ch
Except ISO 13849-1, which applies Markov chains models, the standards analyzed deal with the quantification of safety parameters using Reliability Block Diagrams (RBDs).
IEC 61508-6 provides approximation formulas for the and (low and high demand mode of operations) of simple configurations with no more than three channels.
The main idea of the IEC 61508-6 formulas is to treat a voted group of channels as if the group were a single item. This calculation is based on the average dangerous group failure frequency and the group-equivalent mean downtime , defined differently for low and high demand.
IEC 62061 is based on RBD graphical representations, where the PFH value of the safety function is given by the sum of the PFH values of all subsystems involved in performing the safety function. Another standard that follows this method is IEC DTS 63394.
The feasibility of a standard RBD approach is based on a few coherent simplifications on the nature of our safety related systems, which represents also its limitation in comparison with the complete Markov methods.
nnels.
The main idea of the IEC 61508-6 formulas is to treat a voted group of channels as if the group were a single item. This calculation is based on the average dangerous group failure frequency and the group-equivalent mean downtime , defined differently for low and high demand.
IEC 62061 is based on RBD graphical representations, where the PFH value of the safety function is given by the sum of the PFH values of all subsystems involved in performing the safety function. Another standard that follows this method is IEC DTS 63394.
The feasibility of a standard RBD approach is based on a few coherent simplifications on the nature of our safety related systems, which represents also its limitation in comparison with the complete Markov methods.
Comparison Between RBD and Markov PFH models
With the goal of investigate the adherence between RBD based models and simplified Markov in high demand mode of operations, comparisons that vary the fundamental Functional Safety parameters involved are reported for tested systems.
This approach, as well as being qualitative, aims to investigate which aspects of the model can be further refined or which critical issues are open to further development.
The first of the elements investigated is the Dangerous Failure Rate , also known as , expression of the statistical frequency of dangerous failure for the functional channel. The range of variation selected is coherent with the items generally implied in the industrial applications, starting from to .
The other parameters are fixed and to generalize are selected in , , . The mission time is considered 20 years, while the diagnostic test interval is supposed to be coincident to the average time of the demands and supposed in 1 h (every hour a demand arise and the system test itself).
For the single-channel configuration with diagnostic external to the functional channel (1oo1D), figure 1 demonstrates that the two models present similar trends, despite their different theoretical bases.

Figure 1: RBD (IEC DTS 63394) and Markov (IEC 62061) models comparison for 1oo1D at variable
The discrepancy between RBD and Markov increases as the reliability of the elements worsens. Expanding our comparison range to higher values of λ_D, for example between 10^(-6) and 10^(-4) 1/h , as in figure 2, leads RBD model to generates meaningless negative PFH values. This dynamic is attributable to the model applied to include Common Cause Failures (CCFs). This effect is also shown when β varies at fixed λ_D (figure 3).

Figure 2: RBD (IEC DTS 63394) and Markov (IEC 62061) models comparison for 1oo1D at high λ_D values.

Figure 3: RBD (IEC DTS 63394) and Markov (IEC 62061) models comparison for 1oo1D with variable β .
For the double channel configuration with diagnostic (1oo2D), both models remain adherent (figure 4).

Figure 4: RBD (IEC DTS 63394) and Markov (ISO TC-199) models comparison for 1oo2D at variable λ_D .
The variation of DC and (in 1oo1D) does not influence the relation between RBD and Markov.
1oo2D Structure with Diagnostic External to the Functional Channel
For the dual channel with diagnostic (1oo2D), the standards consider only the case where the diagnostic is managed intrinsically by the functional channel. This aspect is clear following the modelling approaches and from the absence of a failure rate connected to the diagnostic channel in the final formulas, differently from the single monitored channel (1oo1D) where both the cases, internal and external, are evaluated.
A summary of the models proposed for the double channel is reported in figure 5. The effect of diagnostics is evident, which reduces the PFH values and consequently lowers the probability that a dangerous fault will invalidate the safety function of the system.

Figure 5: 1oo2 and 1oo2D with internal fault handling models comparison.
The construction of a model that considers the Fault Handling Function as external (i.e. subjected to failure), complex from a mathematical point of view, would produce worsening curves in the safety performance of the architecture. In particular, these new curves would move, for each model considered, the closer to the double channel without diagnostics (1oo2), the higher the failure rate of the diagnostics itself. The extent of this expected deviation compared to the ideal model must be consistent with what is shown by the comparison between the external and internal diagnostic models for the single channel, according to the models prescribed by the standards.
If we excluded the relationship produced by IEC 61508-6, because of the difference with the IEC DTS 63394 and Markov models (which coincide each other), as observed in the comparison in section 6. the new model will produce a curve included between the curves in black and the curve in blue (figure 5).
An interesting solution, in the absence of a precise mathematical model, can derive from the analysis of the only equation to involve a concept of efficiency linked to diagnostics: that of IEC 61508.
Among the components of the proposed formula, a term K is presented as the Fraction of the Success of the Autotest circuit in the 1oo2D systems, an efficiency quantifying the effectiveness of the detection/reaction mechanism. With this parameter is built a term 2(1-K) λ_Dd that add to PFH a contribute due to the non-ideality of the diagnostic, with which the output may remain on the 2oo2 voting even with one channel detected as faulty. Where λ_Dd represent the fraction of dangerous failure that could be detected by the diagnostic, without degrading the safety performances.
Using this parameter, a modified version of the 1oo2D model according to IEC DTS 63394 or Markov (ISO TC-199) is proposed in equation (4).

The RBD based model modified as above is reported in equation (5).

IEC 61508-6 prescribes the precise estimation of this parameter K through an FMEA analysis.
Without precise information on the frequency of failure of the diagnostic, it is possible to hypothesize a coherent investigation K value, which helps to outline a range of variability for the parameter itself.
Since the monitoring channel is born with this specific function, it is reasonable to expect a high efficiency.
It should also be remembered that the new model will have to operate a reduction of the PFH term with respect to the internal diagnostics that is smaller, in percentage terms, than what happens in the single channel.
If we compare the two structures, 1oo1D and 1oo2D, both with diagnostics external to the functional channel, the diagnostic mechanism for the single channel is fundamental to bring the system to the safe state, while in the dual channel this function is achieved by redundancy.
A conservative value to investigate the applicability of this parameter can be chosen as K=0.99.
In figure 6 it is possible to observe how the new model is positioned in the interval between the curves, as searched and described previously.
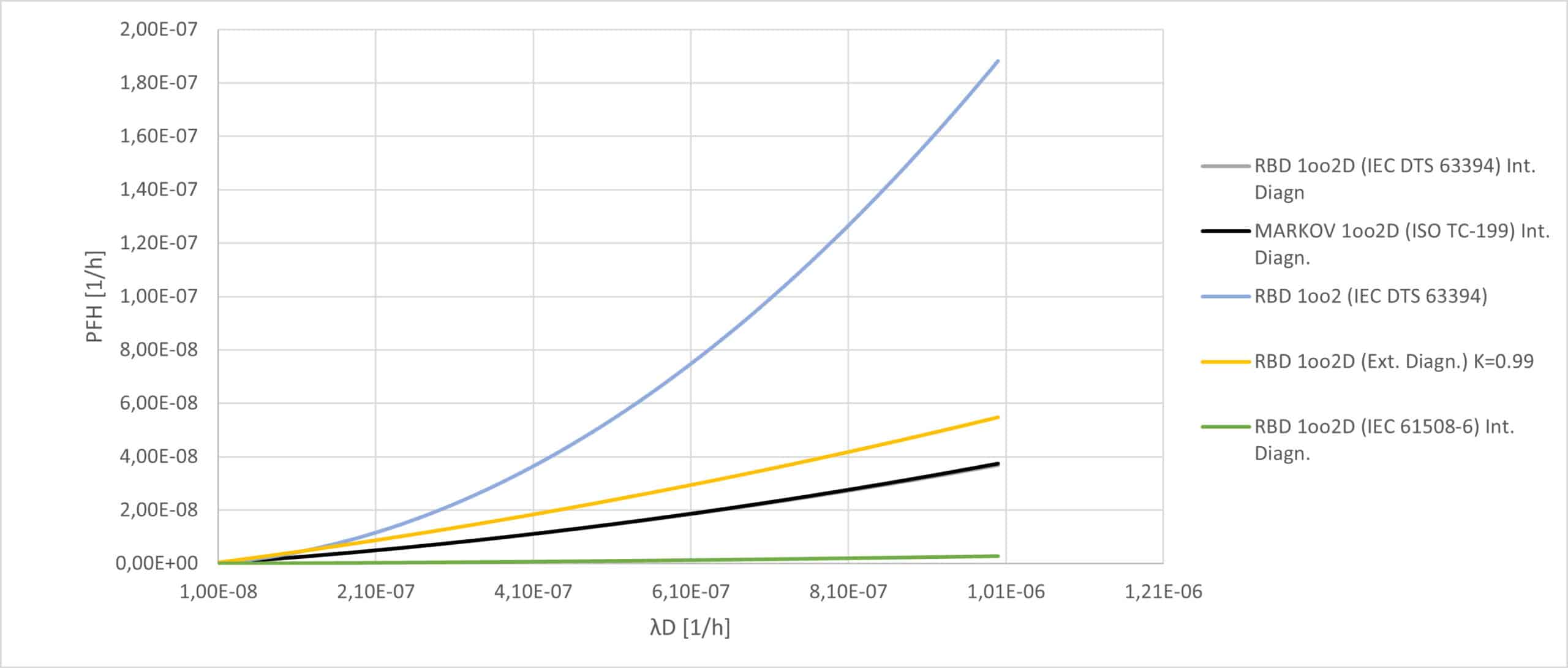
Figure 6: 1oo2 and 1oo2D with external and internal fault handling models comparison.
As the efficiency K decreases the more failures (that normally could be detected and does not participate in terms of safety) are accounted, shifting the curve upwards and producing higher PFH values.
Raising this curve too much, however, as for example using a K between 0.95 and 0.98, would theoretically attribute too much importance to the term PFH linked to diagnostics. Contrary to what happens with dual channel systems, where in presence of a redundancy, the failure of one of the two diagnostic functions could be compensated. Unlike what is observed in the single channel, which model’s comparison is shown as example in figure 7. In this case, the reliability of the diagnostic plays a crucial role in the implementation of the safety function.

Figure 7: 1oo1 and 1oo1D with external and internal fault handling models comparison.
Conclusions and Future Developments
Through this work has been possible to understand the role of Functional Safety within Risk Analysis and its fundamental role in the industry and process world.
The regulatory framework is clear and follows an approach not only numerical but also systematic.
It was shown that a simple method, such as the Reliability Block Diagram (RBD) model, enables to describe a broad spectrum of systems involved in safety functions. Offering results that, within consistently limited ranges of failure rates, can be compared with much more complex relationships such as those of the Markov chains. In addition, RBD can be particularly flexible in offering preliminary solutions to the study of increasingly complex innovative architectures.
This model has been applied to the case of double channel with external diagnostics, a crucial configuration for systems that require particularly high level of safety performances.
The new model investigated offers an alternative perspective: wire all these diagnostic signals to the input cards of an automation PLC and bring only a cumulative signal to the safety one. This solution would be more flexible and cost-effective, particularly for highly complex systems. On the other hand, in doing so, diagnostic systems are introduced that are less efficient and therefore more prone to failure. However, it has been shown, from the simple deduced model, how the weight attributed by the dual channel to diagnostics is almost limited.