P9: Confronto tra i modelli RBD e Markov per l’analisi dei Sistemi di Sicurezza Strumentali

Sommario

In questo articolo sono indagati i principali standard internazionali coinvolti nella Sicurezza Funzionale e come questi applicano la teoria dell’Ingegneria dell’Affidabilità.

In particolare, viene valutata l’applicabilità del metodo dei Reliability Block Diagrams (RBD) analizzando i modelli utilizzati dalle normative e confrontandoli con i risultati ottenibili attraverso il modello delle catene di Markov.

La strategia RBD viene poi utilizzata per studiare una struttura non indagata dagli standard: il doppio canale con diagnostica esterna al canale funzionale.

I risultati, nonostante le approssimazioni e le semplificazioni introdotte, consentono di fornire una soluzione preliminare per questa struttura, coerente con l’intervallo di risultati attesi, che conferma la flessibilità dello strumento presentato, che può rappresentare un metodo per delineare il perimetro di modelli più complessi.

Introduzione

La Sicurezza Funzionale è una parte della procedura di riduzione del rischio associata a una macchina o a un processo protetto dall’implementazione di un Sistema di Controllo di Sicurezza (SCS).

Lo sviluppo di sistemi critici per la sicurezza richiede particolare attenzione poiché l’obiettivo finale è la condizione di sicurezza: rappresentata dall’eliminazione di tutte le energie residue, che potrebbero causare lesioni alle persone, danni alle cose o ripercussioni sull’ambiente.

Una profonda comprensione degli standard coinvolti, di come questi applicano la teoria dell’Ingegneria dell’Affidabilità e dei modelli che sviluppano, rientra nell’ambito di questo articolo.

Ingegneria dell’Affidabilità

La disciplina che studia la capacità di un sistema o di un componente di svolgere una funzione richiesta, in condizioni specifiche e per un dato intervallo di tempo, senza fallire, è l’Affidabilità.

In questa teoria, i guasti sono classificati come casuali o sistematici. I primi possono essere caratterizzati da parametri statistici mentre i secondi mediante un approccio di gestione qualitativo in tutto il ciclo di vita del componente.

Uno dei possibili metodi analitici per valutare l’Affidabilità di un sistema è il Reliability Block Diagram (RBD): un’illustrazione statica mediante blocchi funzionali, che possono essere trattati come equazioni di variabili booleane e la loro Affidabilità calcolata come la probabilità complessiva di successo/fallimento.

Parametri Chiave della Sicurezza Funzionale

L’obiettivo è garantire adeguate prestazioni, durante il tempo di missione, dei componenti coinvolti nelle funzioni di sicurezza; per raggiungere le specifiche definite durante la valutazione del rischio.

Due funzioni possono essere utilizzate per valutare l’Inaffidabilità F(t) di un elemento o sistema, definita come la probabilità che l’elemento o il sistema interrompa la funzione richiesta in un certo momento e collegata all’Affidabilità dall’equazione (1).

In condizioni di bassa richiesta, il parametro utilizzato per indicare l’Inaffidabilità di una funzione di sicurezza è la Probabilità Media di Guasto Pericoloso su Richiesta (PFD_avg)

Nella modalità di funzionamento ad alta richiesta, l’Inaffidabilità è specificata dalla Frequenza Media di un Guasto Pericoloso all’Ora (PFH o PFH_D)

La distinzione tra bassa ed alta richiesta è quantificata dalla normativa nel valore di una richiesta della funzione di sicurezza all’anno.

Standard tecnici sulla Sicurezza Funzionale

IEC 61508 è il principale tra tutti gli standard di prodotto legati alla Sicurezza Funzionale.

Esso consente ai sistemi elettrici/elettronici/programmabili elettronici (E/E/PS) di essere applicati come elementi critici per la sicurezza, specificando quattro livelli di prestazioni di sicurezza (da 1 a 4) denominati Safety Integrity Levels (SIL).

Due standard internazionali, invece, trattano il concetto di sicurezza funzionale applicato ai macchinari: il primo è l’IEC 62061, derivato da IEC 61508, ed il secondo è l’ISO 13849. Entrambi si concentrano su alta richiesta e modalità di funzionamento continua e la quantificazione della riduzione del rischio operata è misurata per IEC in SIL e per ISO in Performance Levels (PL); una relazione tra le due grandezze è riportata nella tabella 1.

Tabella 1: Relazione tra Performance Levels (PL) e Safety Integrity Levels (SIL).

La normativa relativa all’industria di processo è invece l’IEC 61511, che non contiene alcuna formula ma definisce come soddisfare i requisiti di IEC 61508 in un’applicazione di processo (tipicamente in modalità di funzionamento a bassa richiesta).

Il livello più alto che può essere rivendicato da un Sistema di Controllo di Sicurezza (SCS) è limitato da una combinazione di ridondanza, diagnostica ed affidabilità dei componenti. Per facilitare la progettazione o la valutazione del SIL o PL raggiunto, gli standard impiegano una metodologia basata sulla categorizzazione delle architetture, con criteri di progettazione specifici e comportamento in condizioni di guasto (ridondanza). Queste categorie rappresentano le modalità con cui raggiungere uno specifico SIL o PL in un sottosistema, in altri termini descrivono il comportamento richiesto del sottosistema rispetto alla sua resistenza ai guasti.

Modelli di calcolo che coinvolgono gli RBD

Ad eccezione di ISO 13849-1, che applica i modelli delle catene di Markov, gli standard analizzati quantificano i parametri di sicurezza mediante Diagrammi a Blocchi di Affidabilità (RBD).

IEC 61508-6 fornisce formule di calcolo per PFD_avg e PFH (modalità di funzionamento a bassa ed alta richiesta) di configurazioni semplici con non più di tre canali. L’idea principale delle formule di IEC 61508-6 è trattare un gruppo di canali votato come se fosse un singolo elemento. Questo calcolo si basa sulla frequenza media dei guasti pericolosi del gruppo λ_{D, G} e sul tempo di inattività medio equivalente al gruppo t_{i, E}, definiti in modo diverso per bassa ed alta richiesta.

IEC 62061 si basa invece su rappresentazioni grafiche RBD, in cui il valore PFH della funzione di sicurezza è dato dalla somma dei valori PFH di tutti i sottosistemi coinvolti nell’esecuzione della stessa. Un altro standard che segue questa strategia è l’IEC DTS 63394.

La fattibilità di un approccio RBD standard si basa su alcune semplificazioni, coerenti con la natura dei sistemi correlati alla sicurezza, che rappresentano anche il suo limite rispetto ai metodi Markov completi.

Confronto tra i modelli RBD e Markov per il calcolo del PFH

Con l’obiettivo di indagare l’aderenza tra i modelli basati su RBD e Markov semplificato, in modalità di operazione ad alta richiesta, vengono riportati dei confronti al variare dei parametri fondamentali della Sicurezza Funzionale coinvolti nei sistemi analizzati.

Questo approccio, oltre ad essere qualitativo, mira a indagare quali tra gli aspetti del modello possono essere ulteriormente perfezionati o quali questioni critiche sono aperte ad ulteriori sviluppi.

Il primo degli elementi indagati è il Dangerous Failure Rate λ_de, noto anche come λ_D, espressione della frequenza statistica dei guasti pericolosi del canale funzionale. L’intervallo di variazione selezionato è coerente con gli elementi generalmente implicati nelle applicazioni industriali, partendo quindi da 10^-6 a

10^-8 1/h.

Gli altri parametri sono fissi e selezionati, per generalizzare, in DC=0.9, λ_{D_FH}= λ_react = 10^-8 1/h, β = 0.02.

Il tempo di missione T1 è considerato pari a 20 anni, mentre l’intervallo di test diagnostico T2 si suppone coincidente con il tempo medio delle richieste supposto in 1 h (ogni ora si verifica una richiesta ed il sistema esegue il test).

Per la configurazione a singolo canale con diagnostica esterna al canale funzionale (1oo1D), la figura 1 dimostra come i due modelli presentino andamenti simili, nonostante le loro differenti basi teoriche.

Figura 1: Confronto tra i modelli RBD (IEC DTS 63394) e Markov (IEC 62061) per sistema 1oo1D al variare di .

La discrepanza tra modello RBD e Markov aumenta con il peggiorare dell’affidabilità degli elementi. L’ampliamento dell’intervallo di confronto a valori più alti di λ_D, ad esempio tra 10^-6e 10^-41/h, come nella figura 2, porta il modello RBD a generare valori di PFH negativi, fisicamente impossibili. Questa dinamica è attribuibile al modello applicato per includere i guasti per causa comune (CCF) ed è mostrato anche quando β varia a λ_D fisso (figura 3).

Figura 2: Confronto tra i modelli RBD (IEC DTS 63394) e Markov (IEC 62061) per sistema 1oo1D con alti .

Figura 3: Confronto tra i modelli RBD (IEC DTS 63394) e Markov (IEC 62061) per sistema 1oo1D al variare di β.

Per la configurazione a doppio canale con diagnostica (1oo2D), entrambi i modelli rimangono aderenti (figura 4).

Figura 4: Confronto tra i modelli RBD (IEC DTS 63394) e Markov (ISO TC-199) per sistema 1oo2D al variare di λ_D.

La variazione di DC e λreact (in 1oo1D) non influenza la relazione tra RBD e Markov.

Struttura 1oo2D con Diagnostica Esterna al Canale Funzionale

Per il doppio canale con diagnostica (1oo2D), gli standard considerano solo il caso in cui il monitoraggio è gestito internamente al canale funzionale. Questo aspetto è chiaro seguendo gli approcci della modellazione e dall’assenza di un tasso di guasto collegato al canale diagnostico nelle formule finali, diversamente dal singolo canale monitorato (1oo1D) in cui vengono valutati entrambi i casi, interno ed esterno.

Una sintesi dei modelli proposti per il doppio canale è riportata nella figura 5. È evidente l’effetto della diagnostica, che riduce i valori di PFH e di conseguenza abbassa la probabilità che un guasto pericoloso invalidi la funzione di sicurezza del sistema.

Figura 5: Confronto tra i modelli 1oo2 e 1oo2D con diagnostica interna al canale funzionale.

La costruzione di un modello che consideri la Fault Handling Function come esterna (ossia soggetta a dinamica propria), complesso dal punto di vista matematico, produrrebbe un peggioramento nelle curve e quindi nelle prestazioni di sicurezza dell’architettura. In particolare, queste nuove curve si sposterebbero, per ogni modello considerato, tanto più vicino al doppio canale senza diagnostica (1oo2), quanto più elevato è il tasso di guasto della diagnostica stessa. L’entità di questa deviazione attesa rispetto al modello ideale deve essere coerente con quanto mostrato dal confronto tra i modelli di diagnostica esterna ed interna per il singolo canale, utilizzando le equazioni delle norme.

Se escludiamo la relazione prodotta da IEC 61508-6, a causa della differenza con i modelli IEC DTS 63394 e Markov (che coincidono tra loro), come osservato nel confronto nella sezione 6, il nuovo modello produrrà una curva compresa tra la curva in nero e la curva in blu (figura 5).

Una soluzione interessante, in assenza di un modello matematico preciso, può derivare dall’analisi dell’unica equazione che coinvolge un concetto di efficienza legato alla diagnostica: quella della IEC 61508.

Tra i componenti proposti dalla formula, è presentato un termine K definito come Frazione di Successo del circuito Autotest nei sistemi 1oo2D, un’efficienza quindi, che quantifica l’efficacia del meccanismo di rilevamento/reazione.

Con questo parametro è costruito un termine 2(1-K)λ_D che aggiunge al PFH un contributo dovuto alla non idealità della diagnostica, con cui l’output può rimanere 2oo2 anche con un canale rilevato come difettoso. Qui λ_Dd rappresenta la frazione di guasti pericolosi che potrebbe essere rilevato dalla diagnostica, senza degradare le prestazioni di sicurezza.

Utilizzando questo parametro, nell’equazione (4) viene proposta una versione modificata del modello 1oo2D secondo IEC DTS 63394 o Markov (ISO TC-199).

Il modello basato sull’RBD modificato, come sopra, è riportato nell’equazione (5).

La norma IEC 61508-6 prescrive la stima precisa di questo parametro K attraverso un’analisi FMEA.

In assenza di informazioni precise sulla frequenza di fallimento della diagnostica, è possibile ipotizzare un valore di K d’indagine coerente, che aiuti a delineare un intervallo di variabilità per il parametro stesso.

Poiché il canale di monitoraggio nasce con questa specifica funzione, è ragionevole aspettarsi un’elevata efficienza.

Va inoltre ricordato che il nuovo modello dovrà operare una riduzione del termine PFH rispetto alla diagnostica interna che sia inferiore, in termini percentuali, rispetto a quanto avviene nel singolo canale.

Se confrontiamo le due strutture 1oo1D e 1oo2D, entrambe con diagnostica esterna al canale funzionale, il meccanismo di monitoraggio per il singolo canale è fondamentale per portare il sistema allo stato sicuro, mentre nel doppio canale questa funzione è realizzata principalmente dalla ridondanza.

Un valore conservativo per indagare l’applicabilità di questo parametro può essere scelto in K=0,99.

In figura 6 è possibile osservare come il nuovo modello si posizioni nell’intervallo tra le curve, come ricercato e descritto in precedenza.

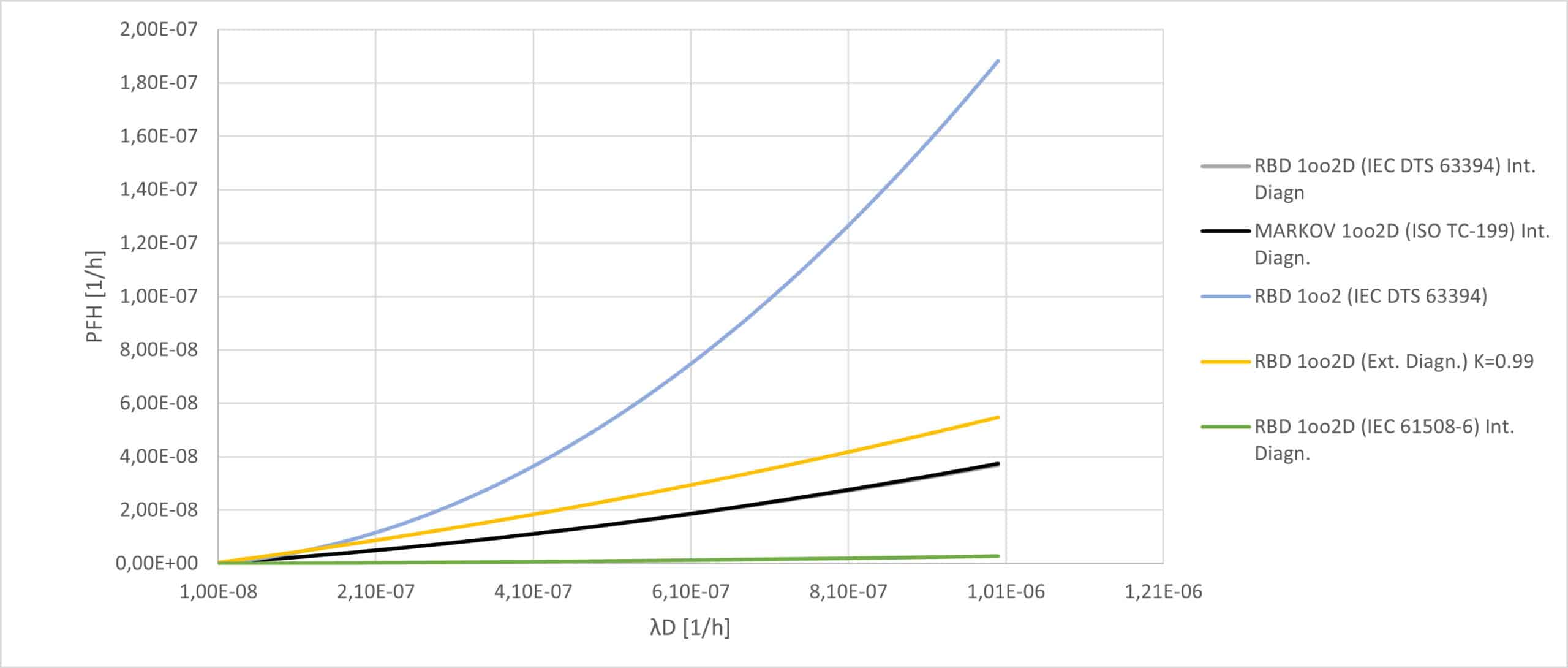
Figura 6: Confronto tra i modelli 1oo2 e 1oo2D con diagnostica esterna ed interna al canale funzionale

Man mano che l’efficienza K diminuisce, vengono presi in considerazione sempre più guasti (che normalmente potrebbero essere rilevati), spostando la curva verso l’alto e producendo valori PFH più elevati.

Innalzare troppo questa curva, tuttavia, come utilizzando un K compreso tra 0,95 e 0,98, attribuirebbe teoricamente troppa importanza al termine PFH legato alla diagnostica. Contrariamente a quanto avviene con i sistemi a doppio canale, dove in presenza di una ridondanza, il fallimento di una delle due funzioni diagnostiche potrebbe essere compensato; diversamente da quanto osservato nel singolo canale, il cui confronto tra i modelli è mostrato come esempio nella figura 7, in questo caso infatti, l’affidabilità della diagnostica gioca un ruolo cruciale nell’implementazione della funzione di sicurezza.

Figura 7: Confronto tra i modelli 1oo1 e 1oo1D con diagnostica esterna ed interna al canale funzionale

Conclusioni e sviluppi futuri

In questo articolo è stato possibile comprendere il ruolo della Sicurezza Funzionale all’interno dell’Analisi di Rischio, fondamentale nel mondo dell’industria e dei processi.

Il quadro normativo è chiaro e segue un approccio non solo numerico ma anche sistematico.

Si è mostrato come il modello dei Reliability Block Diagrams (RBD) consenta di descrivere un ampio spettro di sistemi coinvolti nella sicurezza. Offrendo risultati che, entro intervalli specifici di tassi di guasto, possono essere confrontati con relazioni molto più complesse come quelle delle catene di Markov. Inoltre, gli RBDs possono essere particolarmente flessibili nell’offrire soluzioni preliminari allo studio di architetture innovative sempre più complesse.

Questo modello è stato applicato al caso di doppio canale con diagnostica esterna al canale funzionale, una configurazione cruciale per sistemi che richiedono prestazioni di sicurezza particolarmente elevate.

Il nuovo modello studiato offre una prospettiva alternativa: cablare tutti questi segnali diagnostici alle schede di input di un PLC di automazione e portare solo un segnale cumulativo a quello di sicurezza. Questa soluzione sarebbe più flessibile ed economica, in particolare per sistemi altamente complessi. D’altro canto, così facendo, si introducono sistemi diagnostici meno efficienti e quindi più soggetti a guasti. Tuttavia, è stato dimostrato, dal semplice modello dedotto, come il peso attribuito dal doppio canale alla diagnostica sia limitato, rispetto al singolo canale.