Dernière modification: 04/08/2025
Résumé

Cet article examine les principales normes internationales impliquées dans la Sécurité Fonctionnelle et comment celles-ci appliquent la théorie de l’Ingénierie de la Fiabilité.
En particulier, il évalue l’applicabilité de la méthode des Diagrammes Blocs de Fiabilité (RBD – Reliability Block Diagrams) en analysant les modèles utilisés par les normes et en les comparant aux résultats obtenus à l’aide du modèle des chaînes de Markov.
La stratégie RBD est ensuite utilisée pour étudier une structure non traitée par les normes : le double canal avec diagnostic externe au canal fonctionnel.
Les résultats, malgré les approximations et simplifications introduites, permettent de proposer une solution préliminaire pour cette structure, cohérente avec l’intervalle des résultats attendus, ce qui confirme la flexibilité de l’outil présenté, qui peut représenter une méthode pour délimiter le périmètre de modèles plus complexes.
Introduction
La sécurité fonctionnelle fait partie de la procédure de réduction du risque associée à une machine ou à un procédé, protégés par la mise en œuvre d’un Système de Contrôle de Sécurité (SCS).
Le développement de systèmes critiques pour la sécurité exige une attention particulière, car l’objectif final est d’atteindre une condition de sécurité : celle-ci est représentée par l’élimination de toutes les énergies résiduelles pouvant causer des blessures aux personnes, des dommages aux biens ou des conséquences sur l’environnement.
Une compréhension approfondie des normes concernées, de la manière dont elles appliquent la théorie de l’ingénierie de la fiabilité et des modèles qu’elles développent, fait partie intégrante de cet article.
Ingénierie de la Fiabilité
La discipline qui étudie la capacité d’un système ou d’un composant à accomplir une fonction requise, dans des conditions spécifiques et pendant un intervalle de temps donné, sans défaillance, est la Fiabilité.
Dans cette théorie, les défaillances sont classées en aléatoires ou systématiques. Les premières peuvent être caractérisées par des paramètres statistiques, tandis que les secondes nécessitent une approche de gestion qualitative tout au long du cycle de vie du composant.
L’un des outils analytiques possibles pour évaluer la fiabilité d’un système est le Reliability Block Diagram (RBD) : une illustration statique utilisant des blocs fonctionnels, qui peuvent être traités comme des équations de variables booléennes et dont la fiabilité peut être calculée comme la probabilité globale de succès ou d’échec.
Paramètres Clés de la Sécurité Fonctionnelle
L’objectif est de garantir des performances adéquates, pendant le temps de mission, des composants impliqués dans les fonctions de sécurité, afin d’atteindre les spécifications définies lors de l’évaluation des risques.
Deux fonctions peuvent être utilisées pour évaluer l’Infiabilité F(t) d’un élément ou d’un système, définie comme la probabilité que l’élément ou le système interrompt la fonction demandée à un certain moment, et reliée à la Fiabilité par l’équation (1).

- En conditions de faible demande, le paramètre utilisé pour indiquer l’infiabilité d’une fonction de sécurité est la Probabilité Moyenne de Défaillance Dangereuse à la Demande (PFDavg).

- En mode de fonctionnement à forte demande, l’infiabilité est spécifiée par la Fréquence Moyenne d’une Défaillance Dangereuse par Heure (PFH ou PFHD).

La distinction entre faible et forte demande est quantifiée par la norme selon la valeur d’une demande de la fonction de sécurité par an.
Normes Techniques sur la Sécurité Fonctionnelle
La norme IEC 61508 est la principale parmi toutes les normes de produit liées à la sécurité fonctionnelle.
Elle permet l’utilisation des systèmes électriques/électroniques/électroniques programmables (E/E/PE) comme éléments critiques pour la sécurité, en spécifiant quatre niveaux de performance de sécurité (de 1 à 4), appelés Niveaux d’Intégrité de Sécurité (SIL – Safety Integrity Levels).
Deux normes internationales traitent spécifiquement du concept de sécurité fonctionnelle appliqué aux machines : la première est l’IEC 62061, dérivée de l’IEC 61508, et la seconde est l’ISO 13849.
Toutes deux se concentrent sur les modes de fonctionnement à forte demande ou en continu, et la quantification de la réduction du risque obtenue est mesurée en SIL pour l’IEC et en Niveaux de Performance (PL – Performance Levels) pour l’ISO ; une correspondance entre ces deux grandeurs est présentée dans le tableau 1.

Tableau 1 : Correspondance entre les Niveaux de Performance (PL) et les Niveaux d’Intégrité de Sécurité (SIL).
La norme relative à l’industrie de procédé est l’IEC 61511, qui ne contient aucune formule, mais définit comment satisfaire aux exigences de l’IEC 61508 dans une application de procédé (généralement en mode de fonctionnement à faible demande).
Le niveau le plus élevé pouvant être revendiqué par un Système de Contrôle de Sécurité (SCS) est limité par une combinaison de redondance, de diagnostic et de fiabilité des composants.
Pour faciliter la conception ou l’évaluation du SIL ou du PL atteint, les normes utilisent une méthodologie basée sur la catégorisation des architectures, avec des critères de conception spécifiques et un comportement en conditions de défaillance (redondance).
Ces catégories représentent les moyens d’atteindre un SIL ou un PL spécifique dans un sous-système ; en d’autres termes, elles décrivent le comportement requis du sous-système par rapport à sa résistance aux défaillances.
Modèles de calcul impliquant les RBD
À l’exception de l’ISO 13849-1, qui applique des modèles de chaînes de Markov, les normes analysées quantifient les paramètres de sécurité à l’aide de Diagrammes en Blocs de Fiabilité (RBD – Reliability Block Diagrams).
L’IEC 61508-6 fournit des formules de calcul pour le PFDavg et le PFH (en mode de fonctionnement à faible et forte demande) pour des configurations simples comportant au maximum trois canaux.
L’idée principale des formules de l’IEC 61508-6 est de considérer un groupe de canaux redondants comme un seul élément. Ce calcul est basé sur la fréquence moyenne des défaillances dangereuses du groupe (λD,G) et sur le temps moyen d’indisponibilité équivalent du groupe (ti,E), définis différemment pour les modes à faible et forte demande.
L’IEC 62061, quant à elle, repose sur des représentations graphiques RBD, dans lesquelles la valeur PFH de la fonction de sécurité est obtenue par la somme des PFH de tous les sous-systèmes impliqués dans son exécution.
Une autre norme adoptant cette même stratégie est l’IEC DTS 63394.
La faisabilité d’une approche RBD standard repose sur certaines simplifications, cohérentes avec la nature des systèmes liés à la sécurité, mais qui en constituent également la limite par rapport aux méthodes de Markov complètes.
Comparaison entre les modèles RBD et Markov pour le calcul du PFH
Dans le but d’étudier l’adhérence entre les modèles basés sur RBD et Markov simplifié, en mode de fonctionnement à forte sollicitation, des comparaisons sont effectuées en faisant varier les paramètres fondamentaux de la Sécurité Fonctionnelle impliqués dans les systèmes analysés.
Cette approche, en plus d’être qualitative, vise à examiner quels aspects du modèle peuvent être encore améliorés ou quelles questions critiques restent ouvertes à de futurs développements.
Le premier des éléments étudiés est le Taux de défaillance dangereuse λde, également appelé λD, expression de la fréquence statistique des défaillances dangereuses du canal fonctionnel. L’intervalle de variation sélectionné est cohérent avec les éléments généralement impliqués dans les applications industrielles, allant de 10⁻⁶ à 10⁻⁸ 1/h.
Les autres paramètres sont fixes et sélectionnés, pour généraliser, avec DC=0,9, λD_FH = λreact = 10⁻⁸ 1/h, β = 0,02.
Le temps de mission T₁ est considéré égal à 20 ans, tandis que l’intervalle de test diagnostique T₂ est supposé coïncider avec le temps moyen entre les demandes, estimé à 1 h (une demande survient chaque heure et le système exécute le test).
Pour la configuration à canal unique avec diagnostic externe au canal fonctionnel (1oo1D), la figure 1 montre que les deux modèles présentent des comportements similaires, malgré leurs bases théoriques différentes.

Figure 1 : Comparaison entre les modèles RBD (IEC DTS 63394) et Markov (IEC 62061) pour un système 1oo1D en fonction de λ_D.
La divergence entre le modèle RBD et le modèle de Markov augmente avec la dégradation de la fiabilité des éléments. L’élargissement de l’intervalle de comparaison à des valeurs plus élevées de λD, par exemple entre 10⁻⁶ et 10⁻⁴ 1/h, comme montré dans la figure 2, conduit le modèle RBD à générer des valeurs de PFH négatives, ce qui est physiquement impossible. Cette dynamique est attribuable au modèle utilisé pour inclure les défaillances dues aux causes communes (CCF) et est également observée lorsque β varie à λD fixe (figure 3).

Figure 2 : Comparaison entre les modèles RBD (IEC DTS 63394) et Markov (IEC 62061) pour un système 1oo1D avec des valeurs élevées de λ_D.

Figure 3 : Comparaison entre les modèles RBD (IEC DTS 63394) et Markov (IEC 62061) pour un système 1oo1D en fonction de β
Per la configurazione a doppio canale con diagnostica (1oo2D), entrambi i modelli rimangono aderenti (figura 4).

Figure 4 : Comparaison entre les modèles RBD (IEC DTS 63394) et Markov (ISO TC-199) pour un système 1oo2D en fonction de λD
La variation de DC et de λreact (dans le système 1oo1D) n’influence pas la relation entre les modèles RBD et Markov.
Structure 1oo2D avec diagnostic externe au canal fonctionnel
Pour le double canal avec diagnostic (1oo2D), les normes ne considèrent que le cas où la surveillance est gérée en interne au canal fonctionnel. Cet aspect est clair en suivant les approches de modélisation et l’absence d’un taux de défaillance lié au canal de diagnostic dans les formules finales, contrairement au canal unique surveillé (1oo1D) où les deux cas, interne et externe, sont pris en compte.
Un résumé des modèles proposés pour le double canal est présenté dans la figure 5. L’effet du diagnostic est évident, car il réduit les valeurs de PFH et diminue ainsi la probabilité qu’une défaillance dangereuse invalide la fonction de sécurité du système.

Figure 5 : Comparaison entre les modèles 1oo2 et 1oo2D avec diagnostic interne au canal fonctionnel.
La construction d’un modèle qui considère la fonction de gestion des défaillances (Fault Handling Function) comme externe (c’est-à-dire soumise à une dynamique propre), complexe du point de vue mathématique, entraînerait une dégradation des courbes et donc des performances de sécurité de l’architecture. En particulier, ces nouvelles courbes se rapprocheraient, pour chaque modèle considéré, de plus en plus du double canal sans diagnostic (1oo2), à mesure que le taux de défaillance du diagnostic lui-même augmente. L’ampleur de cette déviation attendue par rapport au modèle idéal doit être cohérente avec ce qui est montré par la comparaison entre les modèles de diagnostic externe et interne pour le canal unique, en utilisant les équations des normes.
Si l’on exclut la relation produite par la norme IEC 61508-6, en raison de la différence avec les modèles IEC DTS 63394 et Markov (qui coïncident entre eux), comme observé dans la comparaison de la section 6, le nouveau modèle produira une courbe comprise entre la courbe noire et la courbe bleue (figure 5).
Une solution intéressante, en l’absence d’un modèle mathématique précis, peut découler de l’analyse de la seule équation impliquant un concept d’efficacité lié au diagnostic : celle de la norme IEC 61508.
Parmi les composants proposés par la formule, un terme K est présenté, défini comme la fraction de succès du circuit d’autotest dans les systèmes 1oo2D, une efficacité donc, qui quantifie l’efficacité du mécanisme de détection/réaction.
Avec ce paramètre est construit un terme 2(1-K)λD qui ajoute au PFH une contribution due à la non-idéalité du diagnostic, avec laquelle la sortie peut rester en mode 2oo2 même avec un canal détecté comme défectueux. Ici, λDd représente la fraction des défaillances dangereuses qui pourrait être détectée par le diagnostic, sans dégrader les performances de sécurité.
En utilisant ce paramètre, dans l’équation (4), une version modifiée du modèle 1oo2D selon IEC DTS 63394 ou Markov (ISO TC-199) est proposée.

Le modèle basé sur le RBD modifié, comme indiqué ci-dessus, est présenté dans l’équation (5).

La norme IEC 61508-6 prescrit une estimation précise de ce paramètre K via une analyse AMDEC (FMEA).
En l’absence d’informations précises sur la fréquence de défaillance du diagnostic, il est possible d’hypothétiser une valeur d’enquête cohérente pour K, afin de délimiter un intervalle de variabilité pour ce paramètre.
Étant donné que le canal de surveillance est conçu avec cette fonction spécifique, il est raisonnable d’attendre une efficacité élevée.
Il convient également de rappeler que le nouveau modèle devra effectuer une réduction du terme PFH par rapport au diagnostic interne qui soit inférieure, en pourcentage, à ce qui se passe dans le canal unique.
Si l’on compare les deux structures 1oo1D et 1oo2D, toutes deux avec diagnostic externe au canal fonctionnel, le mécanisme de surveillance pour le canal unique est fondamental pour amener le système à un état sûr, tandis que dans le double canal cette fonction est principalement réalisée par la redondance.
Une valeur conservatrice pour étudier l’applicabilité de ce paramètre peut être choisie à K = 0,99.
Dans la figure 6, on peut observer comment le nouveau modèle se situe dans l’intervalle entre les courbes, comme recherché et décrit précédemment.
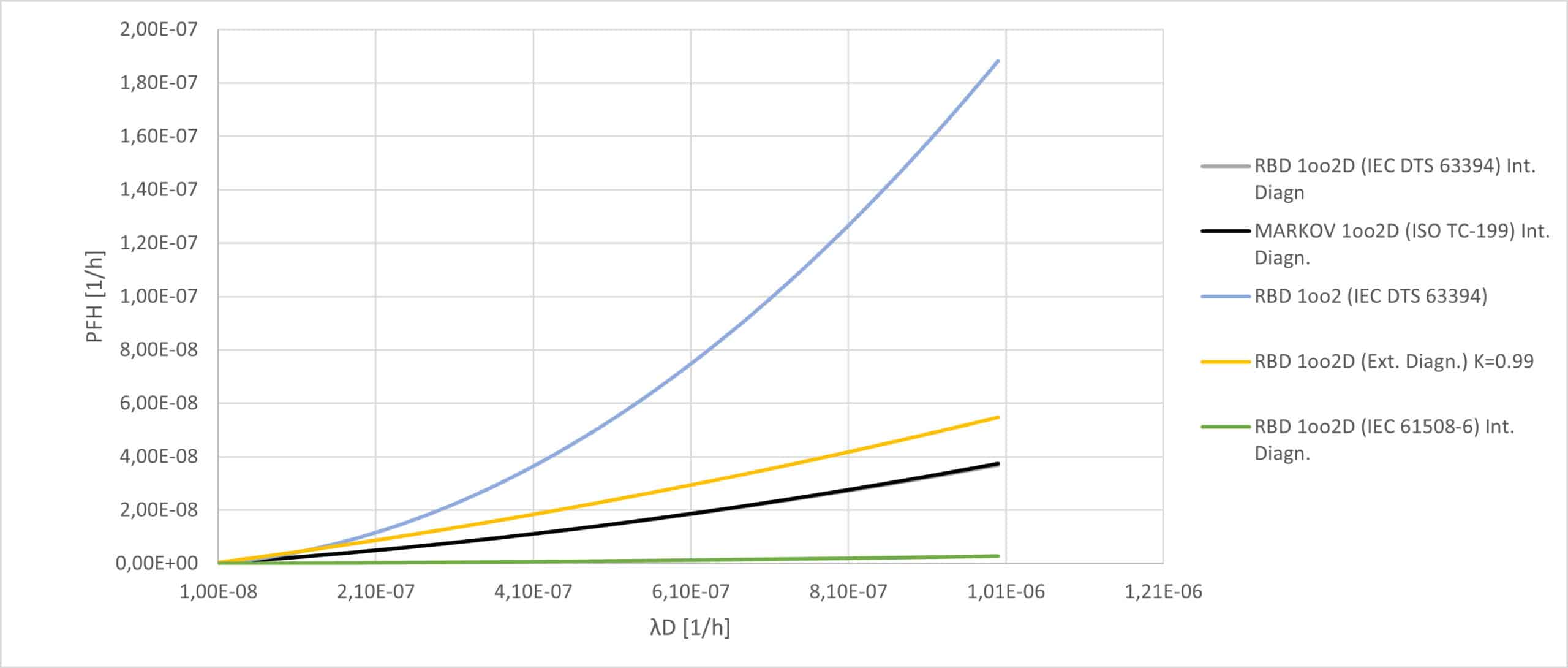
Figure 6 : Comparaison entre les modèles 1oo2 et 1oo2D avec diagnostic externe et interne au canal fonctionnel.
À mesure que l’efficacité K diminue, un nombre croissant de défaillances (normalement détectables) est pris en compte, ce qui fait monter la courbe et produit des valeurs PFH plus élevées.
Cependant, relever trop cette courbe, par exemple en utilisant un K compris entre 0,95 et 0,98, accorderait théoriquement une importance excessive au terme PFH lié au diagnostic. Contrairement aux systèmes à double canal, où en présence de redondance, la défaillance de l’une des deux fonctions de diagnostic pourrait être compensée ; à l’inverse de ce qui est observé pour le canal unique, dont la comparaison entre modèles est montrée à titre d’exemple dans la figure 7, ici, en effet, la fiabilité du diagnostic joue un rôle crucial dans la mise en œuvre de la fonction de sécurité.
Conclusions et développements futurs
Dans cet article, il a été possible de comprendre le rôle de la Sécurité Fonctionnelle dans l’Analyse de Risque, essentielle dans le monde industriel et des procédés.
Le cadre normatif est clair et suit une approche non seulement numérique mais aussi systématique.
Il a été démontré que le modèle des Reliability Block Diagrams (RBD) permet de décrire un large spectre de systèmes impliqués dans la sécurité, offrant des résultats qui, dans des intervalles spécifiques de taux de défaillance, peuvent être comparés à des relations bien plus complexes comme celles des chaînes de Markov. De plus, les RBD sont particulièrement flexibles pour offrir des solutions préliminaires à l’étude d’architectures innovantes de plus en plus complexes.
Ce modèle a été appliqué au cas du double canal avec diagnostic externe au canal fonctionnel, une configuration cruciale pour les systèmes nécessitant des performances de sécurité particulièrement élevées.
Le nouveau modèle étudié offre une perspective alternative : câbler tous ces signaux de diagnostic vers les cartes d’entrée d’un automate programmable industriel (API) et ne transmettre qu’un signal cumulatif à la sécurité fonctionnelle. Cette solution serait plus flexible et économique, en particulier pour des systèmes très complexes. En revanche, cela introduit des systèmes de diagnostic moins efficaces et donc plus sujets aux défaillances. Cependant, il a été démontré, à partir du modèle simple déduit, que le poids attribué par le double canal au diagnostic est limité, comparé au canal unique.